


In this section we describe the data format used for the instances. For illustration we use an odd wheel with terminal nodes 1, 3, 5 and 7.
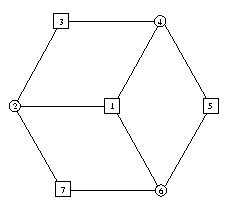
The following lines show this example in the SteinLib format.
33D32945 STP File, STP Format Version 1.0 SECTION Comment Name "Odd Wheel" Creator "T. Koch, A. Martin and S. Voss" Remark "Example used to describe the STP data format" END SECTION Graph Nodes 7 Edges 9 E 1 2 1 E 1 4 1 E 1 6 1 E 2 3 1 E 3 4 1 E 4 5 1 E 5 6 1 E 6 7 1 E 7 2 1 END SECTION Terminals Terminals 4 T 1 T 3 T 5 T 7 END EOF |
The format is line (or row) oriented. Each line is terminated with a line-feed. Everything on a line after (and including) a # is ignored. Blank lines are ignored. The first line of each data file is supposed to be
33D32945 STP File, STP Format Version 1.0
It contains a so-called magic number as an identification key. It provides an assertion that the data file is indeed a file in the SteinLib format. You add this line
0 string 33D32945 STP Steiner Tree Problem File |
Then, the file is divided into sections. A section starts with the keyword SECTION followed by the name of the section and ends with a line containing the keyword END. The file ends with the keyword EOF. The possible sections are shown in the Table and have to appear in the given order.
| Comment | Gives general information about the problem instance, like name and creator. |
| Graph | Here the graph itself is specified. |
| Terminals | Lists the terminals for the problem instance. |
| Coordinates | This is a non-mandatory section giving coordinates for the nodes of the graph. This section is only necessary for drawing. |
Each line within a section starts with a keyword, indicating the type of the line. Depending on the section different keywords are allowed. Each keyword follows a number of fields in the line. Fields can be either a string, i.e. an arbitrary string enclosed in double quotes, or a number, where integer numbers are allowed only.
The following Table lists the keywords for each section. The Column Fields shows how many strings (S) or numbers (N) are required.
| Name | Fields | Description |
|---|---|---|
| Section Comment | ||
| Name | 1 S | The name of the instance |
| Date | 1 S | The date of the creation of the instance |
| Creator | 1 S | Who did it |
| Remark | 1 S | Some other information |
| Problem | 1 S | Default: Steiner Tree Problem in Graphs "Euclidean Steiner Tree Problem", "Rectilinear Steiner Minimum Tree", "Obstacle-Avoiding Rectilinear Steiner Minimum Tree", "Prize-Collecting Steiner Problem in Graphs", "Maximum Node Weight Connected Subgraph" |
| Section Graph | ||
| Obstacles | 1 N | Number of obstacles (for Obstacle-Avoiding Rectilinear Steiner Minimum Tree Problem) |
| Nodes | 1 N | Number of nodes in the graph |
| Edges | 1 N | Number of edges in the graph |
| E | 2 N | Specification of one edge. The number of E lines must match the number given in the Edges line. The two values are Node1 and Node2. The nodes are numbered from one to the number given in the Nodes line. |
| Arcs | 1 N | Number of arcs in the graph |
| A | 3 N | Specification of one arc. The number of A lines must match the number given in the Arcs line. The three values are Tail-Node, Head-Node and Weight. The nodes are numbered from one to the number given in the Nodes line. |
| Section Terminals | ||
| Terminals | 1 N | Number of terminals. Must be between one and the number of Nodes given in the Graph section. |
| RootP | 1 N | Root for Rooted Prize-Collecting Steiner Problem in Graphs |
| Root | 1 N | Node number of the Root-Node for directed Steiner tree problems. |
| T | 2 N | Specification of one terminal. The number of T
lines must match the number given in the Terminals
line. The field specifies the node that is a terminal. The
nodes are numbered from one to the number given in the
Nodes line. Node Weight (Terminal for Maximum Node Weight Connected Subgraph) |
| TP | 1 N | Terminal for (Rooted) Prize-Collecting Steiner Problem in Graphs |
| Section MaximumDegrees | ||
| MD | 1 N | Vertex-degree (Degree-Constrained Steiner Tree Problem in Graphs) |
| Section Coordinates | ||
| D{n} | n N | The number of the values depends on the Dimension. example: DD | 2 N | represents 2D-Cordinates with X- and Y-Coordination. |
Of all sections only Section Graph is compulsory. Within the section Graph we consider either directed or undirected graphs. For directed graphs the keyword Arcs must appear and each line of an arc must start with an A. In addition, the section Terminals must specify a root node. For undirected graphs the keyword Edges gives the number of edges and E lines in the file. The format does not allow mixed graphs as any undirected edge may easily be represented by two anti-parallel arcs with the same end-nodes.
The sections Comment and Coordinates are non-mandatory. If these sections appear to be in the data file, each of their keywords is mandatory itself. Within the section Coordinates all entries must be of the same type. Furthermore, whenever coordinates are given, they must be given for all nodes.

It is possible to include information on the results of preprocessing
in the file. We view the instance specified by the Graph,
Terminal and Coordinates sections as the
problem that is to solve. That means given is the problem that is left
over after any preprocessing.
The amount of information varies
between indicating merely that the instance is the result of some
preprocessing and including all data neccessary to reproduce the
original problem.
Preprocessing information is append to the file by use of another set of sections:
| Comment | Gives general information about the preprocessing program used. |
| Presolve | Here information on the presolving is specified. |
| Terminals | This is a mandatory section listing the terminals of the original instance. |
| Coordinates | This is a non-mandatory section giving coordinates for the nodes of the original graph. This section is only necessary for drawing. |
Original allways means before preprocessing.
Since it is possibly to have several programs preprocess an instance,
the set of preprocessing sections can be repeated.
The fields of the Terminal and Coordinates
sections are the same as above. The Presolve section is
specified as follows:
| Name | Fields | Description |
|---|---|---|
| Section Obstacles | ||
| RR | 4 N | axis-aligned rectangles and described by the coordinates of two opposite corners (x1 y1 x2 y2). (for Obstacle-Avoiding Rectilinear Steiner Minimum Tree Problem) |
| Name | Fields | Description |
|---|---|---|
| Section Presolve | ||
| Fixed | 1 N | The value that must be added to the optimal value of
this preprocessed instance to get the optimal value of the
original instance. The sum of the weights of the
|
| Lower | 1 N | A lower bound. |
| Upper | 1 N | An upper bound. |
| Time | 1 N | Used processing time in seconds. |
| OrgNodes | 1 N | The number of nodes in the original graph. |
| OrgEdges | 1 N | The number of edges in the original graph. |
| EA | 4 N | Description of an aggregated edge. The values are OriginalNode1, OriginalNode2, OriginalWeight, NewEdge. It is possible to have several EA lines with the same value for NewEdge. It is also possible to have several lines with the same values for OriginalNode1, OriginalNode2, OriginalWeight and different values for NewEdge. |
| EC | 3 N | Description of a choosen edge. The values are OriginalNode1, OriginalNode2, OriginalWeight |
| ED | 3 N | Description of an deleted edge. The values are OriginalNode1, OriginalNode2, OriginalWeight |
| ES | 2 N | Description of an edge used for the upper bound. The values are Node1, Node2. If one takes all the EC and ES edges (de-aggregated with according to EA), it should give a valid solution with objective value Upper. Since ES lines are given with actual not original node numbers, the EA lines must be used to find a solution to the original problem. |
If the EA and EC lines for all edges in the orginal graph are given, it is possible to revert a solution to one in the orginal graph. If also all the deleted edges from the orginal graph are given by ED lines, the complete orginal graph can be rebuild. To use EA, EC and ED the OrgNodes and OrgEdges lines must be present. All OriginalNode numbers given in the EA, EC and ED lines must lie between 1 and the number in the OrgNodes line. If EC lines are given, the sum of their weights must be equal to the number given on the Fixed line.
An example is really mising here. ;-)